gated MLP

References:

• Dauphin et al. 2017 https://arxiv.org/abs/1612.08083
• Shazeer 2020 https://arxiv.org/abs/2002.05202
• https://arxiv.org/abs/2402.19427

Where a standard MLP layer is a linear transformation followed by a nonlinearity:

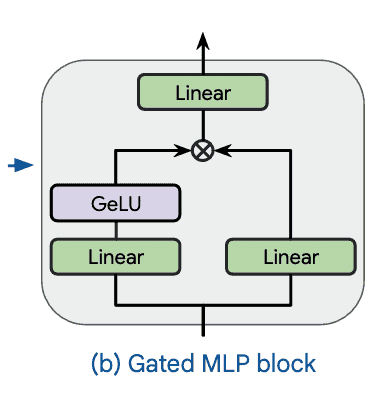
a gated MLP does two linear transformations, applies a nonlinearity to one of them, and multiplies the results (creating a multiplicative interaction):

Equivalently, it does one double-wide transformation, then multiplies one half of the result by a nonlinear transformation of the other half.

In an LSTM-style gate we would effectively have nonlinearities on both factors, e.g., $f(x) = \text{tanh}(xW + b) \otimes \sigma(xV + c)$. Compared to this, the gated MLP can be motivated as having better gradients because it allows for a linear path.

In the context of transformers, Noam Shazeer (https://arxiv.org/abs/2002.05202, 2020) showed that using a gated MLP for the first layer of the feedforward block can improve performance. This works even without the nonlinearity (he calls this a 'bilinear layer') but the best performance comes from a ReLU or a SiLU/Swish nonlinearity: Why would we expect gated layers to work well? Noam Shazeer famously doesn't speculate: "We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence."

Traditional transformer FFN blocks can be interpreted as key-value stores. The first layer $xW_1$ computes dot products of the input 'query' $x$ with keys stored as columns of the weight matrix $W_1$; the output of the block is then a linear combination of 'value' vectors stored in $W_2$, following weights given by the key-query similarity scores (effectively 'normalized' with some sort of nonlinearity). Does using a gated layer change this intuition?

Observation: since $\text{GeLU}(x) = x\Phi(x)$, a gated MLP with GeLU nonlinearity can decompose as